如果你喺無限個步驟之後，放入同拎走波，個樽最後會係空定係滿㗎？

課程摘要

如果你喺無限個步驟之後，放入同拎走波，個樽最後會係空定係滿㗎？

學習路徑

• 第一課：個謎題係咩嚟？
• 第二課：點解會係空？—— 數學家嘅視角
• 第三課：點解會有矛盾？—— 無限嘅奧秘

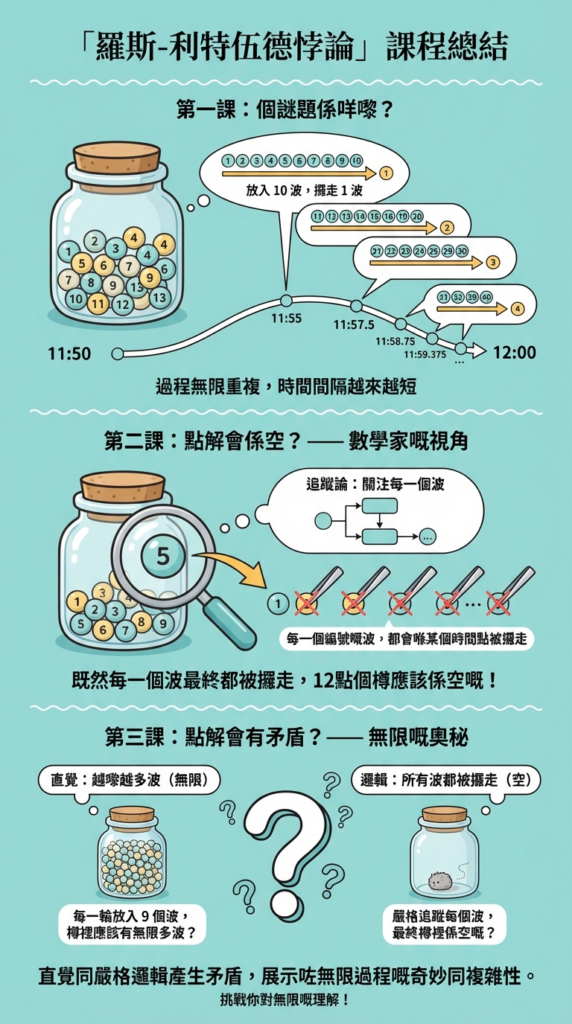
第一課：個謎題係咩嚟？

喂，同學！今日我哋要拆解一個超有嘢嘅腦筋急轉彎——羅斯-利特伍德悖論。想像一下，你面前有一個可以裝無限嘢嘅大樽（叫佢做「無限樽」啦），仲有一大堆波，每個波都獨一無二，上面寫住號碼：1、2、3、4……一直到無限。

而家，我哋玩一個遊戲，呢個遊戲有個術語，叫做「超任務」，意思係指喺有限時間之內，完成無限個步驟。聽上去好似魔法，但跟住我嘅思路嚟。

**遊戲規則係咁樣嘅：**

* **上午 11:50：** 你將 1 號到 10 號波放入個樽，跟住即刻將 1 號波攞走。淨低 2 到 10 號波。
* **上午 11:55：** 你將 11 號到 20 號波放入個樽（而家樽入面有 2-20 號波），跟住即刻將 2 號波攞走。
* **上午 11:57.5：** 你將 21 號到 30 號波放入個樽，跟住即刻將 3 號波攞走。

**重點嚟啦！** 每一次，我哋都將時間縮細一半，放入 10 個新波，然後攞走一個最舊嘅波。咁樣不斷重複，無限次咁做。

**問題就係：** 當時間嚟到正午 12:00 嗰一刻，呢個無限嘅步驟完咗之後，個樽入面到底仲有冇波？如果有，有幾多個？係空、係有限，定係無限呢？

你嘅直覺可能會話：「啱啱放入 10 個，先攞走 1 個，淨低 9 個。無限次之後，應該有無限個波啦！」如果係咁諗，恭喜你，你已經踏入呢個悖論最精彩嘅部分！下一課我哋會用數學同邏輯，睇下呢個直覺係咪啱。

思考題: 根據第一課嘅描述，你直覺上認為正午 12:00 時，個樽入面會係點樣？（唔使答得啱，講下你嘅諗法就得。）

第二課：點解會係空？—— 數學家嘅視角

好，上一課我哋設咗個舞台，而你直覺上可能覺得個樽會滿瀉瀉。但係，如果我哋好似偵探咁，逐一追查每一個波嘅下落，你會發現一個驚人嘅真相。

**我哋用「追蹤法」嚟睇下：**

* **1 號波** 嘅命運係點？佢喺第一步（11:50）被放入，然後即刻喺同一個步驟被攞走。所以，到咗 12:00，1 號波肯定唔喺樽入面。
* **2 號波** 嘅命運係點？佢喺第一步被放入，喺第二步（11:55）被攞走。所以，到咗 12:00，2 號波都唔喺樽入面。
* **3 號波** 嘅命運係點？佢喺第二步被放入，喺第三步（11:57.5）被攞走。

**有冇發現規律？**

對於任何一個波，我哋都可以叫佢做「N 號波」。呢個 N 號波，必定會喺第 N 個步驟被攞走。因為我哋嘅規則就係「喺第 n 個步驟，攞走 n 號波」。

既然我哋嘅遊戲有無限個步驟，噉就代表每一個有具體號碼嘅波（1 號、2 號、3 號、…、100 號、…、一億號、…），無論佢嘅號碼有幾大，都會喺某個特定嘅步驟被攞走。

**所以，當正午 12:00 鐘聲響起，所有無限個步驟都完成之後，** 任何一個你講到出號碼嘅波，都經已喺某個時間點被攞走咗。既然所有嘅波都唔喺度，咁個樽咪空囉！

**呢個就係最令人困惑嘅地方：** 每一個步驟，樽入面嘅波嘅數量都係增加 9 個（加 10 減 1）。點解會喺最後變成 0 個呢？呢個就係「超任務」嘅魔力，亦都係我哋下一課要深入探討嘅核心矛盾。

思考題: 課文話每一個有具體號碼嘅波都會被攞走，所以個樽係空嘅。咁，有冇可能有一啲冇具體號碼嘅波留喺樽入面？點解？

第三課：點解會有矛盾？—— 無限嘅奧秘

歡迎返到最後一課！我哋已經知道兩個完全相反，但聽上去都好有道理嘅結論：
1. **直覺論：** 每步增加 9 個波，無限次之後，應該有無限個波。
2. **追蹤論：** 每一個波都會被攞走，所以個樽應該係空嘅。

點解會咁？問題就出喺我哋點樣理解「無限」呢個概念。

**一個生動嘅比喻：無限酒店**

想像有一間酒店，房間數量係無限嘅，編號係 1、2、3、…。

**情況 A：** 酒店住滿咗客人。而家嚟咗一位新客人，佢有冇房住？有！經理可以透過廣播話：「所有住客，麻煩你搬去你房間號碼加 1 嘅房間。」（1 號房客人搬去 2 號，2 號搬去 3 號…）。噉樣，1 號房就空出嚟，新客人可以入住。呢個情況說明，無限加 1 係等於無限。

**我哋嘅悖論就好似咁：**

我哋嘅「直覺論」就好似話：「你每次都多咗 9 個客人，點會最後冇人？」呢個思維方式，係喺着每一個「瞬間」嘅變化。

但係我哋嘅「追蹤論」，就好似酒店經理咁，佢唔理中間過程有幾混亂，佢只係睇最終名單。佢問：「喺所有客人搬完之後，邊個仲喺名單上？」發現每個人都搬走咗，所以名單係空嘅。呢個思維方式，係睇最終嘅「狀態」。

**矛盾嘅核心：極限 vs. 狀態**

「直覺論」試圖計算一個「極限」（limit）。佢想計 `(9) + (9) + (9) + …` 呢個和嘅極限。但喺數學上，呢個級數係發散嘅，即係話佢嘅極限係「無限大」。問題係，呢個「極限」嘅概念，未必可以直接應用到呢個超任務嘅「最終狀態」上。

「追蹤論」就係直接分析「最終狀態」。佢問：「喺 T=12:00 嗰一刻，邊個波嘅集合係留喺樽入面？」答案係「空集」。

**結論：** 羅斯-利特伍德悖論揭示咗一個深刻嘅數學哲學問題：當我哋處理涉及「無限」嘅過程時，我哋日常用喺「有限」事物上嘅直覺（例如「越嚟越多」同「最後結果」之間嘅關係）可能會失效。過程嘅「極限」同最終嘅「狀態」可以係兩回事。呢個悖論並唔係話數學錯咗，而係提醒我哋，「無限」係一個需要非常小心處理嘅奇怪而美妙嘅世界！

思考題: 如果遊戲規則改咗，每次放 10 個波入去，但係攞走嘅唔係 n 號波，而係隨機攞走一個波，你覺得正午 12:00 時，個樽係空嘅機會大，定係有波嘅機會大？點解？